Exploring Arrows for sequencing effects

Last time, we explored common methods of sequencing effects into little programs. If you haven't read it yet, I'd recommend starting with that, but you can probably manage without it if you insist.

We examined Applicatives, Monads, and Selective Applicatives, and each of these systems had its own trade-offs. We dug into how all approaches exist on the spectrum between being expressive or analyzable and at the end of the post we were unfortunately left wanting something better. Monads reign supreme when it comes to expressiveness as they can express any possible programs we may want to write, but they offer essentially no ability to analyze program they represent without executing it.

On the other hand, Applicatives and Selective Applicatives offered reasonable program analysis, but are unable to express complex programs. They can't even encode programs in which downstream effects materially depend on the results of upstream effects.

These approaches are all based on the same Functor-Applicative-Monad hierarchy, in this post we'll set that aside and rebuild on an altogether different foundation to see if we can do even better.

Setting the goal posts

Before putting in the work let's think critically about the what we felt was missing from the Monad hierarchy and what we wish to gain from a new system.

Here's my wish-list:

• I want to be able to list out every effect that program might perform without executing anything.
• I want to understand the dependencies between the effects including the flow of data between them.
• I want to be able to express programs in which downstream effects can fully utilize the results of upstream effects.

Looking at these requirements, the biggest problem with the Monadic effects system is that it's far too rough-grained in how it handles the results of previous effects. We can see this by reviewing the signature of bind:

(>>=) :: Monad m => m a -> (a -> m b) -> m b

We can see that the result from the previous effect is passed to an arbitrary Haskell function whose job is to return the entire continuation of the program! This permits that function to swap out the entire rest of the program on any particular run, which I'd argue is way more power than the vast majority of reasonable programs require. This is quite frankly a dangerous amount of expressive power, what sort of programs are you writing where you can't even statically identify the possible code paths that might be taken? Even more complex flows like branching, looping and recursion can be expressed in a more structured way without resorting to this sledgehammer level of dynamism.

This tells us we have some room to constrain our programs a bit, and if we're economical about how we do it we can trade that power for the benefits we desire.

We still need to utilize these past results, but we want to avoid opening Pandora's box. That is, we must be careful not to allow the creation of new effects by running arbitrary Haskell functions at execution time. So, in order to use results without a continuation-building function like Monads use, we must meaningfully include the inputs and outputs for our effects in the structure of our effect system itself. We also know that we need to be able to chain these effects together, so we'll need some way to compose them.

If it's not obvious already, this is a great fit for the Category typeclass:

class Category k where
  id :: k a a
  (.) :: k b c -> k a b -> k a c

This already gives us a lot of what we want. Unlike Monads which bake outputs into the continuation of the program using function closures, the Category structure routes inputs and outputs explicitly as part of its structure. Unsurprisingly, it's quite a natural fit; after all, it's called Category Theory, not Monad Theory...

Rebuilding on Categories

Now let's begin to re-implement the examples from the previous post using this new Category-based effect system. In order to save some time, we're actually going to jump up the hierarchy a bit all the way to Arrows.

The Arrow class, if you're not familiar with it, looks like this:

class Category a => Arrow (a :: Type -> Type -> Type) where
  arr :: (b -> c) -> a b c
  (***) :: a b c -> a b' c' -> a (b, b') (c, c')

There are a few other methods we get for free, but this is a minimal set of methods we need to define.

Notice that it has a Category superclass, so we'll use identity and composition from there. We can leverage arr to lift pure Haskell functions into our Category structure. I know we just said we wanted to avoid arbitrary Haskell functions, but note that in this case, just like Applicatives, the function is pure, we can't determine any effects or structure of the effects within the function. No problems here.

We'll re-visit (***) in just a minute.

To get started, how about we re-implement the program we wrote using Applicative in the previous post?

I'll save you from clicking over, here's a refresher on what we did before:

import Control.Applicative (liftA3)
import Control.Monad.Writer (Writer, runWriter, tell)

class (Applicative m) => ReadWrite m where
  readLine :: m String
  writeLine :: String -> m ()

data Command
  = ReadLine
  | WriteLine String
  deriving (Show)

-- | We can implement an instance which runs a dummy interpreter that simply records the commands
-- the program wants to run, without actually executing anything for real.
instance ReadWrite (Writer [Command]) where
  readLine = tell [ReadLine] *> pure "Simulated User Input"
  writeLine msg = tell [WriteLine msg]

-- | A helper to run our program and get the list of commands it would execute
recordCommands :: Writer [Command] String -> [Command]
recordCommands w = snd (runWriter w)

-- | A simple program that greets the user.
myProgram :: (ReadWrite m) => String -> m String
myProgram greeting =
  liftA3
    (\_ name _ -> name)
    (writeLine (greeting <> ", what is your name?"))
    readLine
    (writeLine "Welcome!")

-- We can now run our program in the Writer applicative to see what it would do!
main :: IO ()
main = do
  let commands = recordCommands (myProgram "Hello")
  print commands

-- [WriteLine "Hello, what is your name?", ReadLine, WriteLine "Welcome!"]

The key aspects of this Applicative version were that we could analyze any program which required only an Applicative constraint to get the full list of sequential effects that the program would perform.

Here's the same program, but this time we'll encode the effects using Arrow constraints instead.

But first, a disclaimer: writing Arrow-based programs looks ugly, but don't worry, bear with me for a bit and we'll address that later.

Just like the Applicative version, we'll define a typeclass as the interface to our set of ReadWrite effects, but this time will assume an Arrow constraint:

import Control.Arrow
import Control.Category
import Prelude hiding (id)

class (Arrow k) => ReadWrite k where
  -- Readline has no interesting input, so we use () as input type.
  readLine :: k () String

  -- We track the inputs for the writeLine directly in the Category structure.
  writeLine :: k String ()

-- Helper for embedding a static Haskell value directly into an Arrow
constA :: (Arrow k) => b -> k a b
constA b = arr (\_ -> b)

-- | A simple program which uses a statically provided message to greet the user.
myProgram :: (ReadWrite k) => String -> k () ()
myProgram greeting =
  constA (greeting <> ", what is your name?")
    >>> writeLine
    >>> readLine
    >>> constA "Welcome!"
    >>> writeLine

Great, that should feel pretty straight-forward, it's trivial to convert sequential Applicative programs like this.

In order to run it, we still need to use the IO monad, since that's just how base does IO, but we can use the nifty Kleisli newtype wrapper which turns any monadic computation into a valid Arrow by embedding the monadic effects into the Arrow structure.

Here's how we implement the ReadWrite instance for Kleisli IO:

instance ReadWrite (Kleisli IO) where
  readLine = Kleisli $ \() -> getLine
  writeLine = Kleisli $ \msg -> putStrLn msg

run :: Kleisli IO i o -> i -> IO o
run prog i = do
  runKleisli prog i

And it runs just fine:

>>> run (myProgram "Hello") ()
Hello, what is your name?
Chris
Welcome!

Let's look a little closer at Kleisli:

newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }

Look familiar? It's just the continuation function from monadic bind hiding in there.

There's a difference though, now that arbitrary function is part of our implementation, not our interface!

This is important, because it means we can invent a different implementation of our ReadWrite interface that just tracks the effects that doesn't have to deal with arbitrary binds like this.

Let's implement a command-recorder that does exactly that.

-- Just like the applicative we create a custom implementation of the interface which for static analysis.
-- The parameters are phantom, we won't be running anything, so we only care about
-- the structure of the effects for now.
data CommandRecorder i o = CommandRecorder [Command]

-- We need a Category instance since it's a pre-requisite for Arrow:
instance Category CommandRecorder where
  -- The identity command does nothing, so it records no commands.
  id = CommandRecorder []

  -- Composition of two CommandRecorders just collects their command lists.
  (CommandRecorder cmds2) . (CommandRecorder cmds1) = CommandRecorder (cmds1 <> cmds2)

-- Now the Arrow instance.
instance Arrow CommandRecorder where
  -- We know this function must be pure (barring errors), so we don't
  -- need to track any effects from it.
  arr _ = CommandRecorder []

  -- Don't worry about this combinator yet, we'll come back to it.
  -- For now we'll collect the effects from both sides.
  (CommandRecorder cmds1) *** (CommandRecorder cmds2) = CommandRecorder (cmds1 <> cmds2)

-- | Now implementing the ReadWrite instance is just a matter of collecting the commands
-- the program is running.
instance ReadWrite CommandRecorder where
  readLine = CommandRecorder [ReadLine]
  writeLine = CommandRecorder [WriteLine]

-- | A helper to run our program and get the list of commands it would execute
recordCommands :: CommandRecorder i o -> [Command]
recordCommands (CommandRecorder cmds) = cmds

-- | Here's a helper for printing out the effects a program will run.
analyze :: CommandRecorder i o -> IO ()
analyze prog = do
  let commands = recordCommands prog
  print commands

We can analyze our program and it'll show us which effects it will run if we were to execute it:

>>> analyze (myProgram "Hello")
[WriteLine,ReadLine,WriteLine]

Okay, we've achieved the ability to analyze and execute our program at parity with the Applicative version, but isn't it silly that we're asking the user their name and simply ignoring it? As it turns out, our Arrow interface is quantifiably more expressive: we can use results of past effects in future effects.

Here's something we couldn't do with the Applicative version, we can rewrite the program to greet the user by the name they provide. While we're at it, why not receive the greeting message as an input too?

-- | This program uses the name provided by the user in the response.
myProgram2 :: (ReadWrite k) => k String ()
myProgram2 =
  arr (\greeting -> greeting <> ", what is your name?")
    >>> writeLine
    >>> readLine
    >>> arr (\name -> "Welcome, " <> name <> "!")
    >>> writeLine

Composing arrows lets us route data from one effect to the next, and arr let's us map over values to change them just like fmap does for Functors. The structure of the effects are still statically defined, so even when routing input we can still analyze the entire program ahead of time:

>>> analyze myProgram2
[WriteLine, ReadLine, WriteLine]

>>> run myProgram2 "Hello"
Hello, what is your name?
Chris
Welcome, Chris!

Nifty!

Levelling Up

We're off to a great start, the ability to use the results of past effects is already better than we could get from Selective Applicative, without sacrificing any of the analysis capabilities we had in the Applicative version.

However, at the moment our programs are all still just linear sequences of commands. What happens if we want to route results from an earlier effect down to one far later in the program?

We need a bit more power, time to call back to that (***) we ignored earlier, and while we're at it, let's look at (&&&) too, which we get for free when we implement (***).

(***) :: Arrow k => k a b -> k c d -> k (a, c) (b, d)
(&&&) :: Arrow k => k a b -> k a c -> k a (b, c)

These operators allow us to take two independent programs in our arrow interface and compose them in parallel to one another, rather than sequentially. What parallel means is going to be up to the implementation (within the scope of the Arrow laws), but the key part is that these two sides don't depend on each other, which is distinct from the normal sequential composition we've been doing with (>>>).

With these we can write a now write a slightly more complex program which routes values around, and can forward values from earlier effects to later ones.

import UnliftIO.Directory qualified as Directory

-- The effects we'll need for this example
class (Arrow k) => FileCopy k where
  readLine :: k () String
  writeLine :: k String ()
  copyFile :: k (String, String) ()

data Command
  = ReadLine
  | WriteLine
  | CopyFile
  deriving (Show)

-- Here's the real executable implementation
instance FileCopy (Kleisli IO) where
  readLine = Kleisli $ \() -> getLine
  writeLine = Kleisli $ \msg -> putStrLn msg
  copyFile = Kleisli $ \(src, dest) -> Directory.copyFile src dest

-- Helper prompting the user for input.
prompt :: (FileCopy cat) => String -> cat a String
prompt msg =
  pureC msg
    >>> writeLine
    >>> readLine

fileCopyProgram :: (FileCopy k) => k () ()
fileCopyProgram =
  ( prompt "Select a file to copy"
      &&& prompt "Select the destination"
  )
    >>> copyFile

This program prompts the user for a source file and a destination file, then copies the source file to the destination. Notably, each prompt is independent of one another, that is, they don't have any data-dependencies on one another. But, copyFile takes two arguments, the results of each prompt. (&&&) allows us to express this.

Let's run it:

>>> run fileCopyProgram ()
Select a file to copy
ShoppingList.md
Select the destination
ShoppingList.backup

Uhh, okay so you can't see the result, but trust me it works! Kleisli's implementation of (***) just runs the left side, then the right side; but if, for other applications, you wanted real parallel execution you could write your implementation which runs each pair of parallel operations using Concurrently or something like it and your program will magically become as parallel as your data-dependencies allow! Caveat emptor, but at least having the option is nice, we don't get that from the Monadic interface where data-dependencies are hidden from us.

Now for the analysis.

We could, of course, still collect and print out the list of effects that would be run, but I'm bored of that, so let's level that up too. Now that we have both sequential and parallel composition, our programs are a tree of operations, so our analysis tools should probably follow suite.

Here's a rewrite of our CommandRecorder which tracks the whole tree of effects:

-- | We can represent the effects in our computations as a tree now.
data CommandTree eff
  = Effect eff
  | Identity
  | Composed (CommandTree eff {- >>> -}) (CommandTree eff)
  | -- (***)
    Parallel
      (CommandTree eff) -- First
      (CommandTree eff) -- Second
  deriving (Show, Eq, Ord, Functor, Traversable, Foldable)

data CommandRecorder eff i o = CommandRecorder (CommandTree eff)

instance Category (CommandRecorder eff) where
  -- The identity command does nothing, so it records no commands.
  id = CommandRecorder Identity

  -- I collapse redundant 'Identity's for clarity.
  -- The category laws make this safe to do.
  (CommandRecorder Identity) . (CommandRecorder cmds1) = CommandRecorder cmds1
  (CommandRecorder cmds2) . (CommandRecorder Identity) = CommandRecorder cmds2
  (CommandRecorder cmds2) . (CommandRecorder cmds1) = CommandRecorder (Composed cmds1 cmds2)

instance Arrow (CommandRecorder eff) where
  -- We don't bother tracking pure functions, so arr is a no-op.
  arr _f = CommandRecorder Identity

  -- Track when we fork into parallel execution paths as part of the tree.
  (CommandRecorder cmdsL) *** (CommandRecorder cmdsR) = CommandRecorder (Parallel cmdsL cmdsR)

-- | The interface implementation just tracks the commands
instance FileCopy (CommandRecorder Command) where
  readLine = CommandRecorder (Effect ReadLine)
  writeLine = CommandRecorder (Effect WriteLine)
  copyFile = CommandRecorder (Effect CopyFile)

analyze :: CommandRecorder Command i o -> IO ()
analyze prog = do
  let commands = recordCommands prog
  putStrLn $ renderCommandTree commands

Now we can build the tree of effects, let's take advantage of that and render it as a tree too!

Here's a function that renders any program tree down into a flow-chart description using the mermaid diagramming language.

Don't judge me for the implementation of my mermaid renderer... In fact, if you have a nicer one please send it to me :)

(It's not terribly important, so feel free to skip it)

diagram :: CommandRecorder Command i o -> IO ()
diagram prog = do
  let commands = recordCommands prog
  putStrLn $ commandTreeToMermaid commands

-- | A helper to render our command tree as a flow-chart style mermaid diagram.
commandTreeToMermaid :: forall eff. (Show eff) => CommandTree eff -> String
commandTreeToMermaid cmdTree =
  let preamble = "flowchart TD\n"
      (outputNodes, links) =
        renderNode cmdTree
          & flip runReaderT (["Input"] :: [String])
          & flip evalState (0 :: Int)
   in preamble
        <> unlines
          ( links
              <> ((\output -> output <> " --> Output") <$> outputNodes)
          )
  where
    newNodeId :: (MonadState Int m) => m Int
    newNodeId = do
      n <- get
      put (n + 1)
      return n
    renderNode :: CommandTree eff -> ReaderT [String] (State Int) ([String], [String])
    renderNode = \case
      Effect cmd -> do
        prev <- ask
        nodeId <- newNodeId
        let cmdLabel = show cmd
            nodeDef = show nodeId <> "[" <> cmdLabel <> "]"
            links = do
              x <- prev
              pure $ x <> (" --> " <> nodeDef)
        pure ([nodeDef], links)
      Identity -> do
        nodeId <- newNodeId
        prev <- ask
        let nodeDef = show nodeId <> ("[Identity]")
        let links = do
              x <- prev
              pure $ x <> (" --> " <> nodeDef)
        pure ([nodeDef], links)
      Composed cmds1 cmds2 -> do
        (leftIds, leftNode) <- renderNode cmds1
        (rightIds, rightNode) <- local (const leftIds) $ renderNode cmds2
        pure (rightIds, leftNode <> rightNode)
      Parallel cmds1 cmds2 -> do
        prev <- ask
        nodeId <- newNodeId
        let nodeDef = show nodeId <> ("[Parallel]")
        (leftIds, leftNode) <- local (const [nodeDef]) $ renderNode cmds1
        (rightIds, rightNode) <- local (const [nodeDef]) $ renderNode cmds2
        let thisLink = do
              x <- prev
              pure $ x <> (" --> " <> nodeDef)
            links =
              thisLink
                <> leftNode
                <> rightNode
        pure (leftIds <> rightIds, links)

Here's what the diagram output for our fileCopyProgram looks like:

>>> diagram fileCopyProgram
flowchart TD
Input --> 0[Parallel]
0[Parallel] --> 1[WriteLine]
1[WriteLine] --> 2[ReadLine]
0[Parallel] --> 3[WriteLine]
3[WriteLine] --> 4[ReadLine]
2[ReadLine] --> 5[CopyFile]
4[ReadLine] --> 5[CopyFile]
5[CopyFile] --> Output

And rendered:

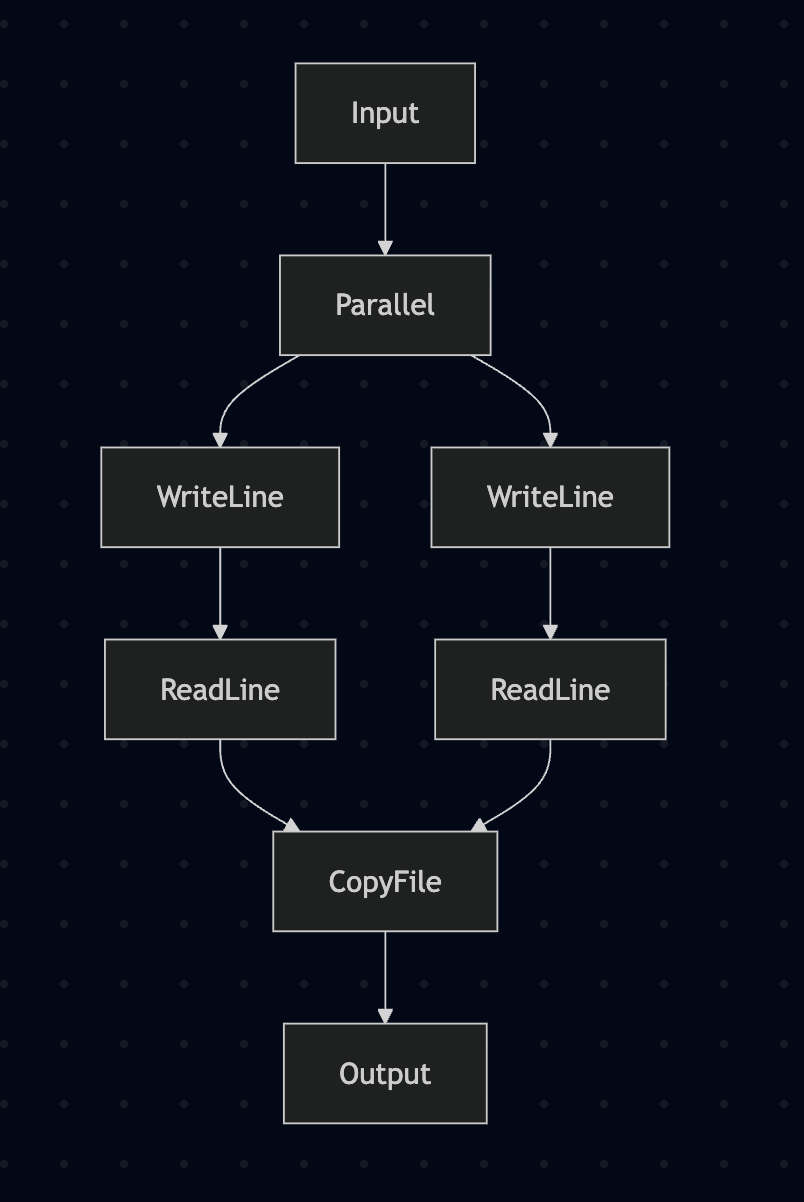
Pretty cool eh?

Diagramming is just one thing you can do with our CommandTree, it's just data, you can fold over it to get all the effects, analyze which effects depend on which others, all sorts of things. This provides more clarity into what's happening than Selective's Over and Under newtypes.

This was a very simple example, but I promise you, with combinations of arr, (***) and first/second you can do any possible routing of values that you might like.

What you can't do yet, however, is to branch between possible execution paths, then run only one of them.

Let's add that.

Branching with ArrowChoice

Luckily for us, adding branching is pretty straight-forward. There's an aptly named ArrowChoice in base that we'll go ahead and implement.

ArrowChoice adds a new combinator:

(+++) :: ArrowChoice k => k a b -> k c d -> k (Either a c) (Either b d)

Similar to how (***) lets us represent two parallel and independent programs and fuse them into a single arrow which runs both, (+++) lets us introduce a conditional branch to our program, only one path will be executed based on whether the input value is a Left or a Right.

By implementing (+++) we also get the similar (|||) for free:

(|||) :: ArrowChoice k => k a c -> k b c -> k (Either a b) c

Let's add a Branch case to our CommandTree and implement ArrowChoice for our CommandRecorder.

data CommandTree eff
  = Effect eff
  | Identity
  | Composed (CommandTree eff {- >>> -}) (CommandTree eff)
  | Parallel
      (CommandTree eff) -- First
      (CommandTree eff) -- Second
  | Branch
      (CommandTree eff) -- Left
      (CommandTree eff) -- Right
  deriving (Show, Eq, Ord, Functor, Traversable, Foldable)

instance ArrowChoice (CommandRecorder eff) where
  (CommandRecorder cmds1) +++ (CommandRecorder cmds2) = CommandRecorder (Branch cmds1 cmds2)

No problem. As a reminder, here's the branching program we expressed using Selective Applicatives last time:

-- | A program using Selective effects
myProgram :: (ReadWriteDelete m) => m String
myProgram =
  let msgKind =
        Selective.matchS
          -- The list of values our program has explicit branches for.
          -- These are the values which will be used to crawl codepaths when
          -- analysing your program using `Over`.
          (Selective.cases ["friendly", "mean"])
          -- The action we run to get the input
          readLine
          -- What to do with each input
          ( \case
              "friendly" -> writeLine ("Hello! what is your name?") *> readLine
              "mean" ->
                let msg = unlines [ "Hey doofus, what do you want?"
                                  , "Too late. I deleted your hard-drive."
                                  , "How do you feel about that?"
                                  ]
                 in writeLine msg *> deleteMyHardDrive *> readLine
              -- This can't actually happen.
              _ -> error "impossible"
          )
      prompt = writeLine "Select your mood: friendly or mean"
      fallback =
        (writeLine "That was unexpected. You're an odd one aren't you?")
          <&> \() actualInput -> "Got unknown input: " <> actualInput
   in prompt
        *> Selective.branch
          msgKind
          fallback
          (pure id)

This example was always a bit forced just because of how limited Selective Applicatives are, but let's copy it over into our Arrow setup anyways.

First we'll implement ArrowChoice for our CommandRecorder.

-- Define our effects
class (Arrow k) => ReadWriteDelete k where
  readLine :: k () String

  writeLine :: k String ()

  deleteMyHardDrive :: k () ()

-- New commands for the new effects
data Command
  = ReadLine
  | WriteLine
  | DeleteMyHardDrive
  deriving (Show)

-- Track the effects
instance ReadWriteDelete CommandRecorder where
  readLine = CommandRecorder (Pure ReadLine)
  writeLine = CommandRecorder (Pure WriteLine)
  deleteMyHardDrive = CommandRecorder (Pure DeleteMyHardDrive)

-- Here's the runnable implementation
instance ReadWriteDelete (Kleisli IO) where
  readLine = Kleisli $ \() -> getLine
  writeLine = Kleisli $ \msg -> putStrLn msg
  deleteMyHardDrive = Kleisli $ \() -> putStrLn "Deleting hard drive... Just kidding!"

And here's our program which uses ArrowChoice:

branchingProgram :: (ReadWriteDelete k, ArrowChoice k) => k () ()
branchingProgram =
  pureC "Select your mood: friendly or mean"
    >>> writeLine
    >>> readLine
    >>> mapC
      ( \case
          "mean" -> Left ()
          "friendly" -> Right ()
          -- Just default to friendly
          _ -> Right ()
      )
    >>> let friendly =
              pureC "Hello! what is your name?"
                >>> writeLine
                >>> readLine
                >>> mapC (\name -> "Lovely to meet you, " <> name <> "!")
                >>> writeLine
            mean =
              pureC
                ( unlines
                    [ "Hey doofus, what do you want?",
                      "Too late. I deleted your hard-drive.",
                      "How do you feel about that?"
                    ]
                )
                >>> writeLine
                >>> deleteMyHardDrive
         in mean ||| friendly

Notice again, this version is actually more expressive than the Selective Applicative version, it actually greets the user by the name they provided, how kind.

I'll elide the edits to the mermaid renderer, Branch is very similar to the implementation of Parallel.

Let's make a mermaid chart like before:

>>> diagram branchingProgram
flowchart TD
Input --> 0[WriteLine]
0[WriteLine] --> 1[ReadLine]
1[ReadLine] --> 2[Branch]
2[Branch] --> 3[WriteLine]
3[WriteLine] --> 4[DeleteMyHardDrive]
2[Branch] --> 5[WriteLine]
5[WriteLine] --> 6[ReadLine]
6[ReadLine] --> 7[WriteLine]
4[DeleteMyHardDrive] --> Output
7[WriteLine] --> Output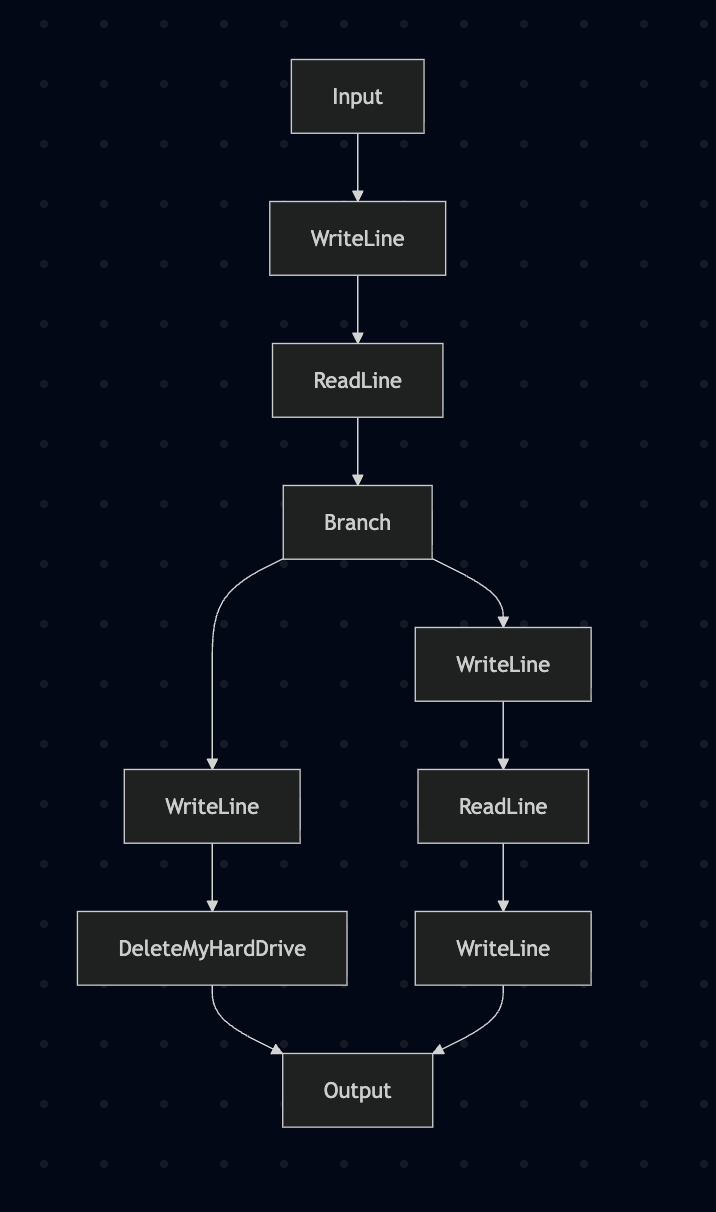

See how it's now clear that the effects on one branch differ from another?

And of course we can run it just as you'd expect:

>>> run branchingProgram
Select your mood: friendly or mean
friendly
Hello! what is your name?
Joe
Lovely to meet you, Joe!

>>> run branchingProgram
Select your mood: friendly or mean
mean
Hey doofus, what do you want?
Too late. I deleted your hard-drive.
How do you feel about that?

Deleting hard drive... Just kidding!

Okay, so the syntax of that last example was starting to get pretty hairy, if only there was something like do-notation, but for arrows...

Arrow Notation

By enabling the {-# LANGUAGE Arrows #-} pragma we can use a form of do-notation with arrows. It will automatically route your inputs wherever you need them using combinators from the Arrow class and will even translate if and case statements into ArrowChoice combinators, it's very impressive.

I won't explain Arrow Notation deeply here, so go ahead and check out the GHC Manual for a more detailed look.

Here's what our branching program looks like when we translate it:

branchingProgramArrowNotation :: (ReadWriteDelete k, ArrowChoice k) => k () ()
branchingProgramArrowNotation = proc () -> do
  writeLine -< "Select your mood: friendly or mean"
  mood <- readLine -< ()
  case mood of
    "mean" -> mean -< ()
    "friendly" -> friendly -< ()
    _ -> friendly -< ()
  where
    friendly = proc () -> do
      writeLine -< "Hello! what is your name?"
      name <- readLine -< ()
      writeLine -< "Lovely to meet you, " <> name <> "!"

    mean = proc () -> do
      writeLine
        -<
          unlines
            [ "Hey doofus, what do you want?",
              "Too late. I deleted your hard-drive.",
              "How do you feel about that?"
            ]
      deleteMyHardDrive -< ()

It takes a bit of getting used to, but it's not so bad.

Here's the diagram, so we can get an idea of how it's being translated:

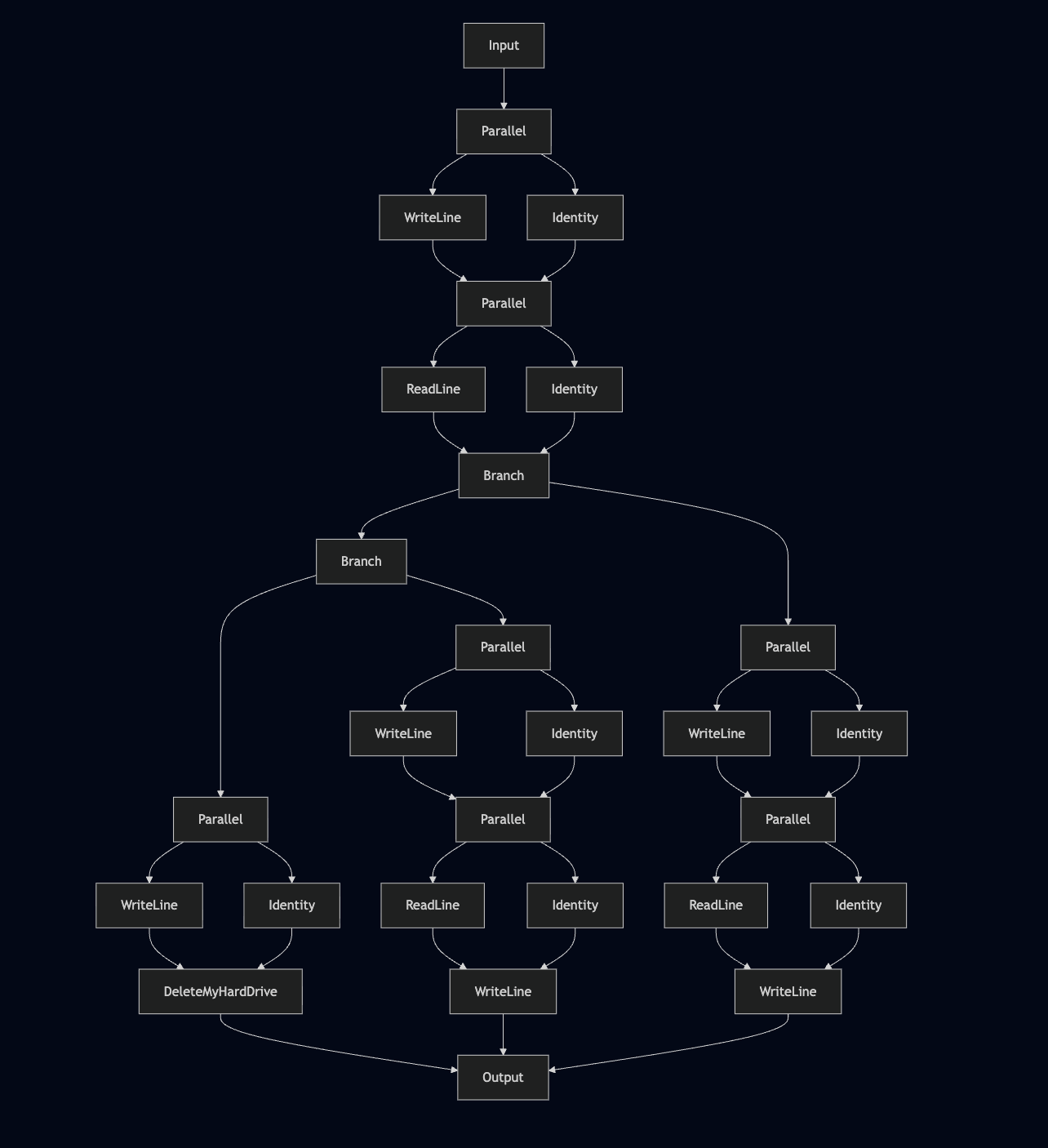
It's not quite as pretty, the translation introduces a lot of unnecessary calls to Parallel where it's just inserting Identity on the other side, this is perfectly valid, since the Category laws require that the Identity won't affect behaviour, but in our case it's messy and is clogging up our diagram, so let's clean it up.

The command tree we build as an intermediate step is just a value, so we can transform it to clean it up no problem.

If you derive Data and Plated for our Command and CommandTree types then we can do this with a simple transform on the tree. transform will rebuild the tree from the bottom up removing any redundant Identity nodes as it goes.

unredundify :: (Data eff) => CommandTree eff -> CommandTree eff
unredundify = transform \case
  Parallel Identity right -> right
  Parallel left Identity -> left
  Branch Identity right -> right
  Branch left Identity -> left
  Composed Identity right -> right
  Composed left Identity -> left
  other -> other

Diagramming the unredundified version looks much cleaner:

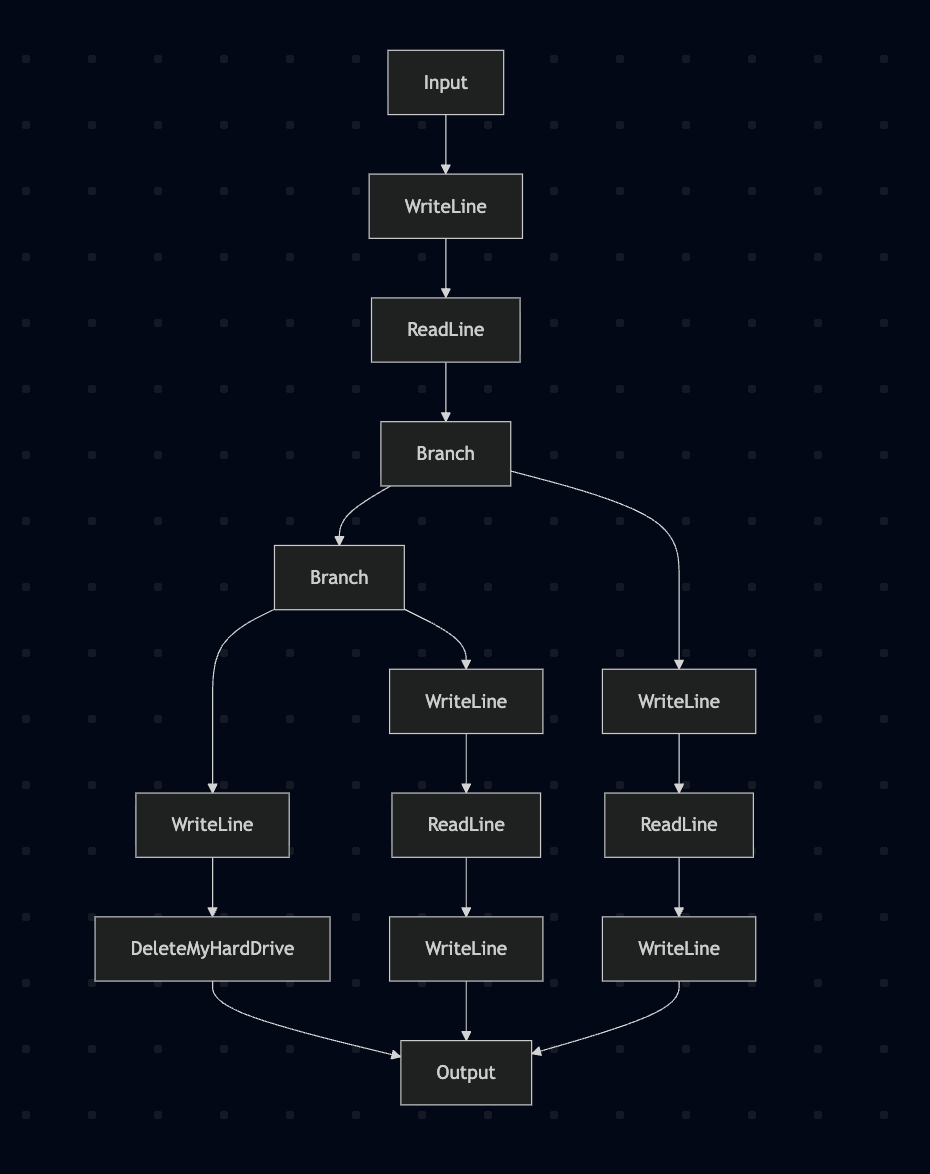
We can see here that case statements with multiple arms are getting collapsed into a sequence of binary branches, which is perfectly correct of course, but if you wanted to diagram it as a single branch you could rewrite the Branch constructor to have a list of options and collapse them all down with another rewrite rule. Same for Parallels of course. You can really do whatever is most useful for your use-case.

Arrow notation has its quirks, but it's still a substantial improvement over doing argument routing completely manually.

Static vs Dynamic data

It's worth a quick note on the difference between static and dynamic data with Arrows. With Applicatives, all the data needed to define an effect's behaviour was static, that is, it must be known at the time the program was constructed, though this might still be at runtime for the greater Haskell program.

With Arrows it's possible to interleave static and dynamic data, it's up to the author of the interface.

For example, if one were constructing a build-system they might have an interface like this:

class (Arrow k) => Builder k where
  dynamicReadFile :: k FilePath String
  staticReadFile :: FilePath -> k () String

dynamicReadFile takes its FilePath as a dynamic input, so we won't know which file we're going to read until execution time, however staticReadFile takes its FilePath as a static input. You pass it a single FilePath as a Haskell value when you construct the program. In this case we can embed the FilePath into the structure of the effect itself so that it's available during analysis.

While this is a bit more of an advanced use-case, it can be very useful. In the build-system case you could provide any statically known dependency files using staticReadFile and the build-system could check if those files have changed since the last run and safely replace some subtrees of the build with cached results if no dependencies in that subtree have changed.

This sort of thing takes careful thought and design, but provides a lot of flexibility which can unlock whole new programming techniques.

Folks may well have heard of Haxl, it's a Haskell library for analyzing programs and batching and caching requests to remote data sources. The implementation and interface for Haxl is moderately complex, and is limited in what it can do by the fact that it uses Monads. I'm curious how effective an Arrow-based version could be.

What's next?

We explored enough classes to enable most basic programs here. At this point you can branch, express independence between computations, and route input anywhere you need it. In case you're still hankering for a bit more expressive power we'll do a lightning quick tour of a few more classes.

There's ArrowLoop which encodes fixed-point style recursion.

class Arrow a => ArrowLoop a where
  loop :: a (b, d) (c, d) -> a b c

Interestingly, this is actually just another name for Costrong, as you can see by comparing with Costrong from the profunctors package.

If you really really need to be able to completely restructure your program on the fly you can do so using the ArrowApply class, which enables applying arbitrary runtime-created arrows.

class Arrow a => ArrowApply a where
    app :: a (a b c, b) c

This gives you the wildly expressive power to define entirely new code-paths at runtime. I'd still argue that reasonable programs that actually need to do this are pretty rare, but sometimes it's a useful shortcut to avoid some tedium. Note that if you use app, any effects within the dynamically applied arrow will be hidden from analysis, but you can still analyze the non-dynamic parts.

There are a few additional interesting classes which are strangely missing from base; but they have counterparts in profunctors. One example would be an arrow counterpart to Cochoice, which, if it existed, would look something like this:

class (Arrow k) => ArrowCochoice k where
  unright :: k (Either d a) (Either d b) -> k a b
  unleft :: k (Either a d) (Either b d) -> k a b

While the behaviour ultimately depends on the implementation, you can use this to implement things like recursive loops and while-loops, which avoids one of the more common needs for ArrowApply while preserving analysis over the contents of the loop.

There's some other good stuff in profunctors so I'd recommend just browsing around over there, (Thanks Ed). Traversing lets you apply a profunctor to elements of a Traversable container, Mapping does the same for Functors.

Anyways, you can see that most behaviours you take for granted when writing Haskell code with arbitrary functions in do-notation binds can generally be decomposed into some combination of Arrow typeclasses which accomplish the same thing. Using the principal of least-power is a good rule of thumb here. Generally you should use the lowest-power abstraction you can reasonably encode your program with, that will ensure you'll have the strongest potential for analysis.

In Summary

We've discovered that by switching from the Functor-Applicative-Monad effect system to a Category and Arrow hierarchy we can express significantly more complex and expressive programs while maintaining the ability to deeply introspect the programs we create.

We learned how we can collect additional typeclasses to gain more expressive power, and how we can implement custom instances to analyze and even diagram our programs.

Lastly we took a look at Arrow notation and how it improves the burden of syntax for writing these sorts of programs.

So, should we all abandon Monads and write everything using Arrows instead? Truthfully, I do believe they comprise a better foundation; so while the current Haskell ecosystem is all-in on Monads, if you the reader happen to be designing the effects system for a brand new functional programming language, why not give Arrows a try?

Hopefully you learned something 🤞! If you did, please consider joining my Patreon to keep up with my projects, or check out my book: It teaches the principles of using optics in Haskell and other functional programming languages and takes you all the way from an beginner to wizard in all types of optics! You can get it here. Every sale helps me justify more time writing blog posts like this one and helps me to continue writing educational functional programming content. Cheers!